A Quick Dive into Heat Transfer (II)

Phew, it has been a while since I last updated my blog. Sorry, world!

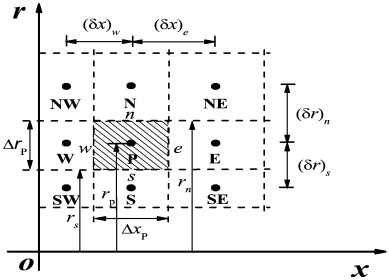
So, in my last post I (sort of) detailed a quasi-static mathematical model of the heat flow of a steel prism as it undergoes a quenching process.

In order to not be overly obnoxious with the mathematical formulae, I will use this post to explain how I approached this problem from a programming perspective.

A Gauss Seidel Solver

Let's create a Flowchart depicting what our Gauss-Seidel solver will do to resolve the matrix-based equations we previously found:

Note that the condition for simulation finished is a bit up in the air. In my case, I assume that the simulation is finished when the earliest of these two occurs:

• Total simulation time has elapsed 300 seconds.
• The temperature differential between the inside and the outside of the prism is less than 30 degrees.

The full version of all code used here can be found in my GitHub

A naive implementation of a 3-D Matrix in C++ could look something like:

class Matrix {
public:
  Matrix(unsigned int xSize, unsigned int ySize, unsigned int zSize, double initialValue) {
    m_matrix.resize(m_size_x);
    for (unsigned x = 0; x < m_matrix.size(); x++) {
        m_matrix[x].resize(m_size_y);
        for (unsigned y = 0; y < m_matrix[x].size(); y++) {
            m_matrix[x][y].resize(m_size_z, initialValue);
        }
    }
  }
  
private:
  std::vector<std::vector<std::vector<double>>> m_matrix;
}

This implementation has multiple issues:

• Memory allocation is very inefficient, as we are allocating memory chunks iteratively, instead of a single call memory allocation.
• Any operation we need to perform on a matrix will perform poorly, since we must access three vectors to get to a single element.

To solve these problems, let's flatten this 3D matrix into a 1D vector, and define a mapping function, at that will map a 3-D element (x,y,z) into an element number W in the 1D vector.

// Matrix.h
class Matrix {
public:
    Matrix(unsigned int xSize, unsigned int ySize, unsigned int zSize, double initialValue);
    double at(const unsigned &, const unsigned &, const unsigned &) const;
private:
    unsigned m_size_x;
    unsigned m_size_y;
    unsigned m_size_z;

    std::vector<double> m_matrix;
};

// Matrix.cpp
double Matrix::at(const unsigned int & x, const unsigned int & y, const unsigned int & z) const{
    return m_matrix[x + m_size_x * (y + m_size_y * z)];
}

Then, all we've left is to implement the Gauss Seidel iterative solver. In my implementation I decided to create a Solver class, which takes some values driving convergence as parameters. It instantiates a physical model class, designed to describe the geometric structure of the steel prism to quench.

When I originally built this project back in 2011, I could not get the solver to converge. It bugged me so much that 10 years later I decided to try to implement it again, and finally found the root cause of the lack of convergence. You see, the Gauss-Seidel method's convergence is only guaranteed if the matrix is either strictly diagonally dominant, or symmetric and positive definite. This problem does fulfill those requirements, so what was the issue?

Let's take a look at this chunk of code, comments included:

double Solver::Cp(unsigned int x, unsigned int y, unsigned int z) {
    //Cp = -5561.455 + 53.22458*temp - 0.1940006*temp^2 + 0.0003336*temp^3 - 2.548565e-7*temp^4 + 6.988594e-11*temp^5
    double temp = ActiveMatrix()->operator()(x,y,z);
    /*
     if(temp>1273.0) { return 350.0;}
    if(temp>1173.15 && temp<=1273.15) { return 1100.0;}
    if(temp>1073.15 && temp<=1173.15) { return 1800.0;}
    if(temp>973.15 && temp<=1073.15) { return 2400.0;}
    if(temp>873.15  && temp<=973.15) { return 2600.0;}
    if(temp>673.15  && temp<=873.15)  { return 2300.0;}
    if(temp>573.15  && temp<=673.15)  { return 1500.0;}
    if(temp>473.15  && temp<=573.15)  { return 900.0;}
    if(temp>373.15  && temp<=473.15)  { return 550.0;}
    if(temp>273.15  && temp<=373.15)  { return 150.0;}
      */
    //return 400.0;
    double Cp = -5561.455 + 53.22458*temp - 0.1940006*pow(temp,2.0) + 0.0003336*pow(temp,3.0) - 2.548565e-7*pow(temp,4.0) + 6.988594e-11*pow(temp,5.0);
    return Cp;
}

Initially, I had defined the thermal conductivity function as a non-continuous function. When running a simulation, the nodes within the steel slowly made their way to lower temperatures, yielding situations where there would be neighboring nodes with drastically different specific heats. When iterating on a given time step, the sudden changes of Cp meant the solver got permanently stuck trying to resolve the temperatures for that specific time step.